
オームの法則を使って電流を求められるけど
回路が分岐していたらどうなるの?

分岐したそれぞれの抵抗値に応じて分かれて流れるよ。
分流
電流は抵抗の少ない部分つまり、流れやすい部分を通る性質があります。
抵抗が並列接続されている場合には抵抗値の低い方に大きい電流が流れて、抵抗値の高い方には小さい電流が流れるようになります。
これを分流といいます。
回路に流れる電流は並列抵抗の合成抵抗と電源電圧から求めますが、
その電流が抵抗の値に応じて分けて流れるので、分流された電流を合計すると
元の電流値になります。
回路全体に流れる電流は増えることも減ることもありません。
例題

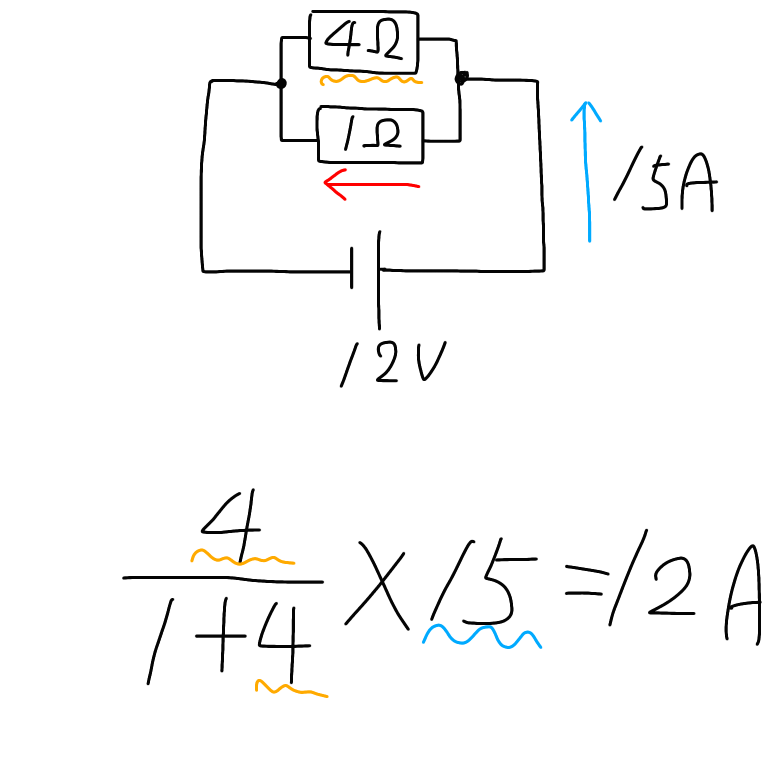
4Ωと1Ωの抵抗が並列に接続されていて電源電圧は12Vの回路があります。
並列接続された抵抗の合成抵抗をまずは求めていきます。
そこから回路全体に流れる電流がわかります。
その後にそれぞれの抵抗に分かれて流れる電流を計算します。
合成抵抗と回路の全電流
上の図の回路の合成抵抗は、和分の積を用いて計算すると、
4/5=4÷5=0.8Ωが求められます。
回路の全電流は12V÷0.8Ω=15Aと求められます。
1Ω側に流れる電流
回路の全電流が分かったら、1Ωの抵抗に流れる電流を求めます。
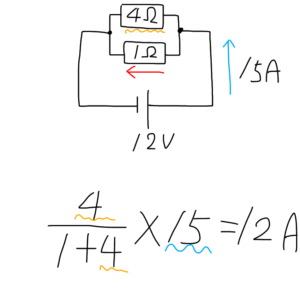
分母が2個の抵抗の足し算で分母が逆側の抵抗値、回路の全電流を掛けることで求められます。
4/5×15=12
1Ωの抵抗には12Aの電流が流れます。
4Ω側に流れる電流
同じ計算式を使って計算すると、
1/5×15=3Aとなります。
逆比の関係
全電流がわかっていれば抵抗の比で電流の比を求めることもできます。
抵抗が4:1です。それぞれの流れる電流は抵抗の逆比になります。
電流比は1:4になります。15Aの電流をこの比で割り振ることになります。
比の計算をわかりやすく説明
1:4は元の数値を分けた比率です。
5等分してそれぞれ1つと4つに分けたことになります。
15Aをまず5等分します。
それが3Aです。それぞれ1倍と4倍にすれば求まります。
抵抗の小さい方に大きい電流が流れることだけ間違えないでください。
比の分配のイメージがしっかりできていれば難しい計算をしなくても直感的に
解けるようになります。
分流された電流の合計
それぞれの電流値を足すと、回路の全電流15Aとなることになります。
1Ω側に12A、4Ω側に3Aの電流が流れます。
小さい抵抗側に多くの電流が流れることがわかります。
第二種電気工事士の資格を目指す方へ
第二種電気工事士は計算問題はありますが難解な問題は少なく(計算問題自体少ないです)
独学でも十分に合格ができる資格です。
受験資格はなくだれでも挑戦でき、合格後は職場を問わず役に立ちます。
ぜひ取得して自分の活躍できるチャンスを広げていってほしいと思います。



コメント