【初心者け】簡単にわかるクーロンの法則

電気の勉強を始めたとき最初の高いハードルになるのがクーロンの法則だと思います。

学習を始めたばかり、悩んでいる方向けに解説していきたいと思います。

クーロンの法則

クーロンの法則は電荷間に働く静電力を示した法則です。

二つの電荷が引き合う（反発しあう）力を静電力またはクーロン力といいます。

[mathjax]

$$ 静電力=\frac{(Q_a)\times(Q_b)}{4πr^2ε_0}$$

式に表すとこのように表現されます。

帯電した物体を帯電体といいます。

帯電体の持つ電気量を電荷といい、プラスの正電荷とマイナスの負電荷があります。

電荷の持つ電気量の単位がクーロン[C]が使われます。記号はQで表されます。

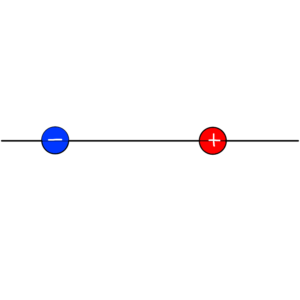
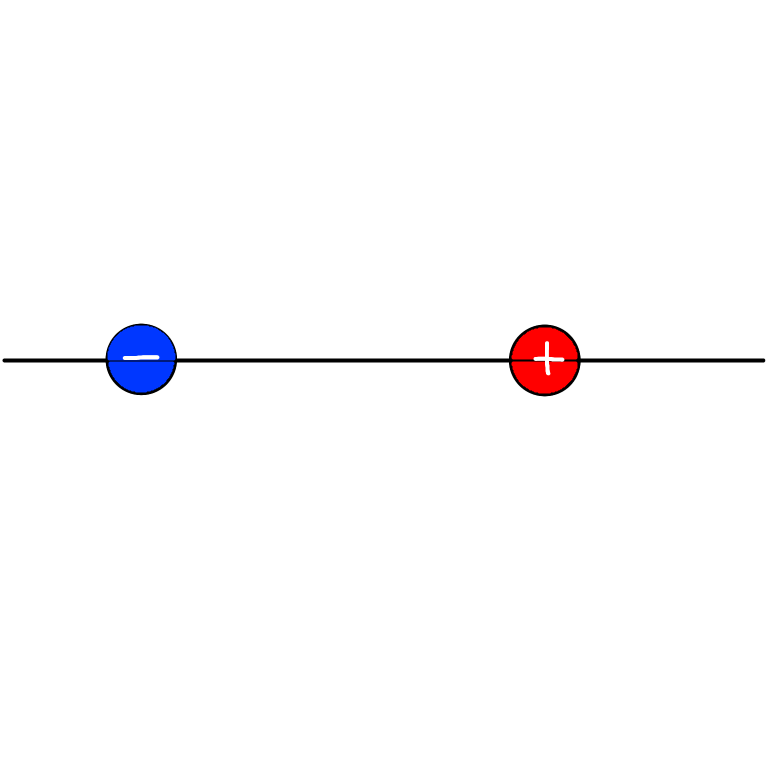
プラス(Q)とマイナス(-Q)の二つの電荷があります。
電荷を一つの点にみなしてよい場合、点電荷といいます。

二つの点電荷はプラスとマイナスの電荷、異なる符号なのでお互いに引き寄せ合います。
この二つの電荷が同じ符号の場合は反発しあいます。

この電荷が大きいほど引き合う力は強くなり、距離が近いほど力が強くなります。

二つの電荷間に発生する力は電荷同士を結ぶ直線上に沿って働きます。

電荷量の単位は[C]クーロン、記号はQで表されます。
Q[C]と表記されます。

クーロンの法則

二つの電荷が距離ｒの距離にある時に発生する静電力は
$$ 静電力=k\times\frac{(Q_a)\times(Q_b)}{r^2}$$

kは比例定数なので条件下で一定の数値となります
$$ k=\frac{1}{4πε_0}=およそ9\times10^9$$

$ε_0＝8.85\times10^{-12}$は真空中の誘電率です。
円周率と誘電率を代入して計算するとおよそ$$9\times10^9$$になります。

比例定数kに代入して変形すると

$$ 静電力=\frac{(Q_a)\times(Q_b)}{4πr^2ε_0}$$

と表せます。