オームの法則と並列回路と直列回路の考え方を使った問題です。
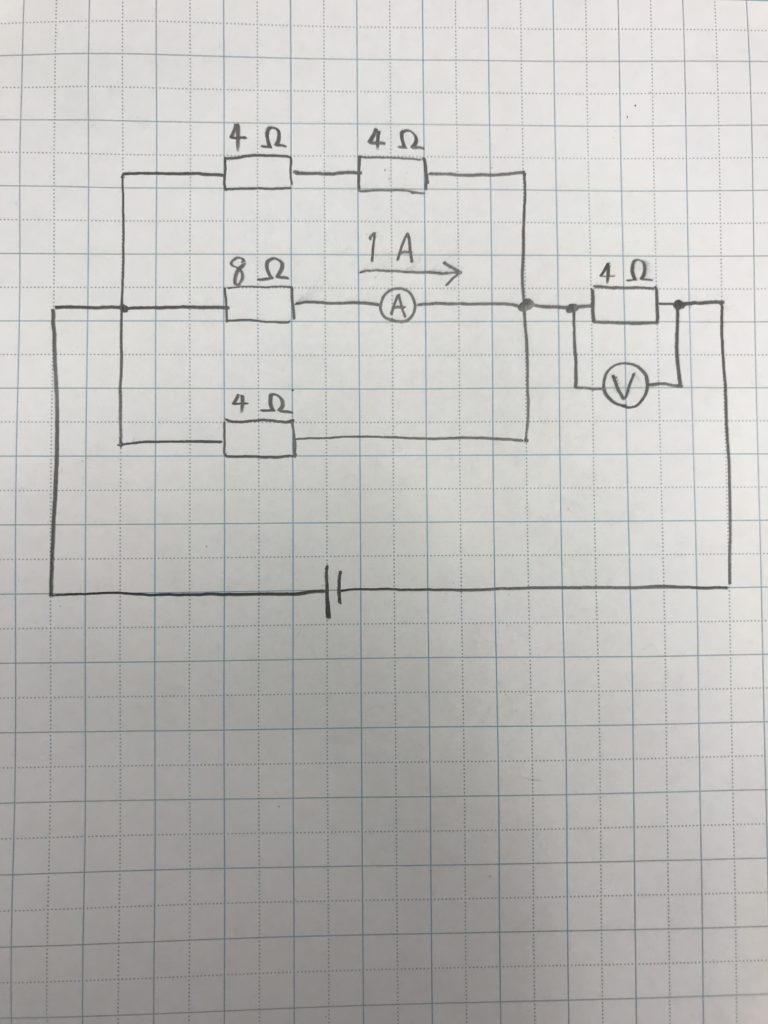
8Ωの抵抗につながる電流計が1Aを示したとき、電圧計が何Vを示すかといった問題です。
〇で囲まれたAが電流計、〇で囲まれたVが電圧計です。
与えられた数値から回答に必要なポイントを押さえて
計算していくことが必要です。
無駄な計算をできるだけ省くことも大事です。
左側の並列回路から考えていきます。
まず8Ωの抵抗に1Aが流れているので
オームの法則(電圧=電流×抵抗)から8Vが掛かっていることが求められます。
また並列回路には等しく電圧がかかるので、
4Ωが2個の回路及び4Ω単体の回路にも8Vがかかることが分かります。
4Ωの抵抗が2個直列なので合成抵抗は8Ωなので、
ここには1Aの電流が流れます。
4Ω単体の回路には2Aが流れることがオームの法則を用いて
求めることができます。
回路全体に流れる電流は、並列回路にそれぞれ分かれた電流の合計になるので、足し合わせると4Aになります。
電圧計が接続された4Ωの抵抗には4Aが流れることになります。
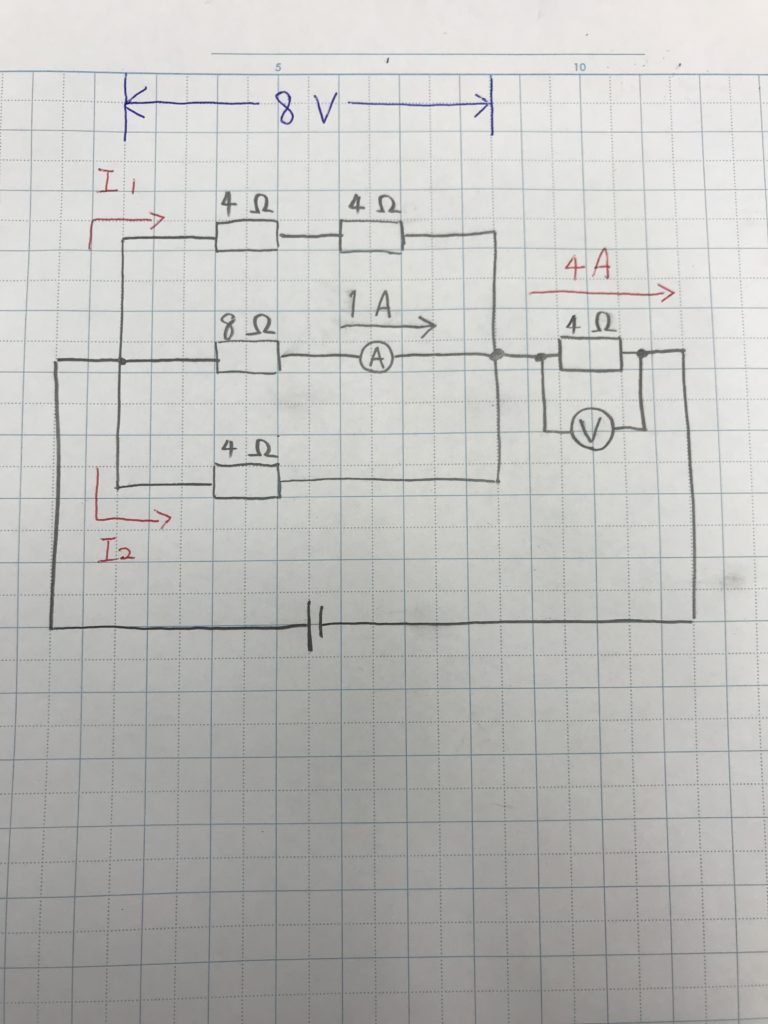
4Ω×4Aなので16Vが回答になります。
また、序盤の並列回路の計算は電気抵抗は電気の流れにくさ
と目をつけると、直感的に考えることができます。
4Ω2個の直列は合成抵抗8Ωなので中央の8Ωと同じ電流がながれることはすぐわかると思います。
一番下の4Ω単体のかいろは8Ωの半分の抵抗値です。
抵抗が半分なので電流は2倍流れるので2Aになります。
電流の流れやすさ、流れにくさに注目すると、計算しなくても、計算の手順が簡単になります。



コメント