【電気数学】簡単にわかる弧度法と度数法の基本の関係【ラジアン】

円の1周の角度は何度ですか？

360度です。

度数法とは違った円の角度の表し方があって、
電気数学では弧度法というものがよく使用されます。

弧度法って何ですか？

円周上にできる弧の長さを使って角度を表現するものです。

円周の求め方

円の円周の求め方は直径×πです。
※半径×2=直径です。

半径が1の円の円周を求めてみます。

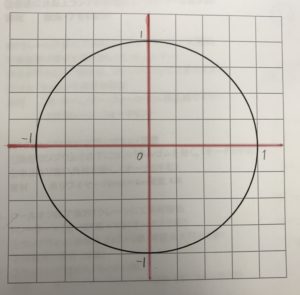
半径が1なので直径は2になります。それにπをかけるので円周の長さは
2πと求められます。

πってなんだ？

円周率は3.14から始まるどこまでも続いていく数値です。
それを記号πに置き換えて計算しやすくしています。

円周率とは円周に対する直径の割合のことですが、
わかりやすくいうと直径を3.14倍するとおよそ円周の長さとなります。

これは円の大きさに関わらず円周率は変わらない不思議な性質があります。

360°の理由

古代バビロニアにおいて使われていた暦に由来し、
30日×12カ月で太陽が同じ場所になっていることに気づいてこれを
1年と設定したのが起源のようです。

360という数字

約数がとても多く24個もあります。
そして10までの数字では7以外のすべての数で割ることができます。
また10進数、12進数、60進数で割ることができ非常に便利な数字です。

ただ円の角度が360であることに数学的な理由はなく、実務上便利なため
使用されてきたといえると思います。

ラジアン（rad）

ラジアン=弧の長さ÷半径となります。

なので半径に対して弧の長さが二倍でありば2ラジアンとなります。
言い換えるとラジアンは弧の長さに比例しています。

度数法と弧度法の関係

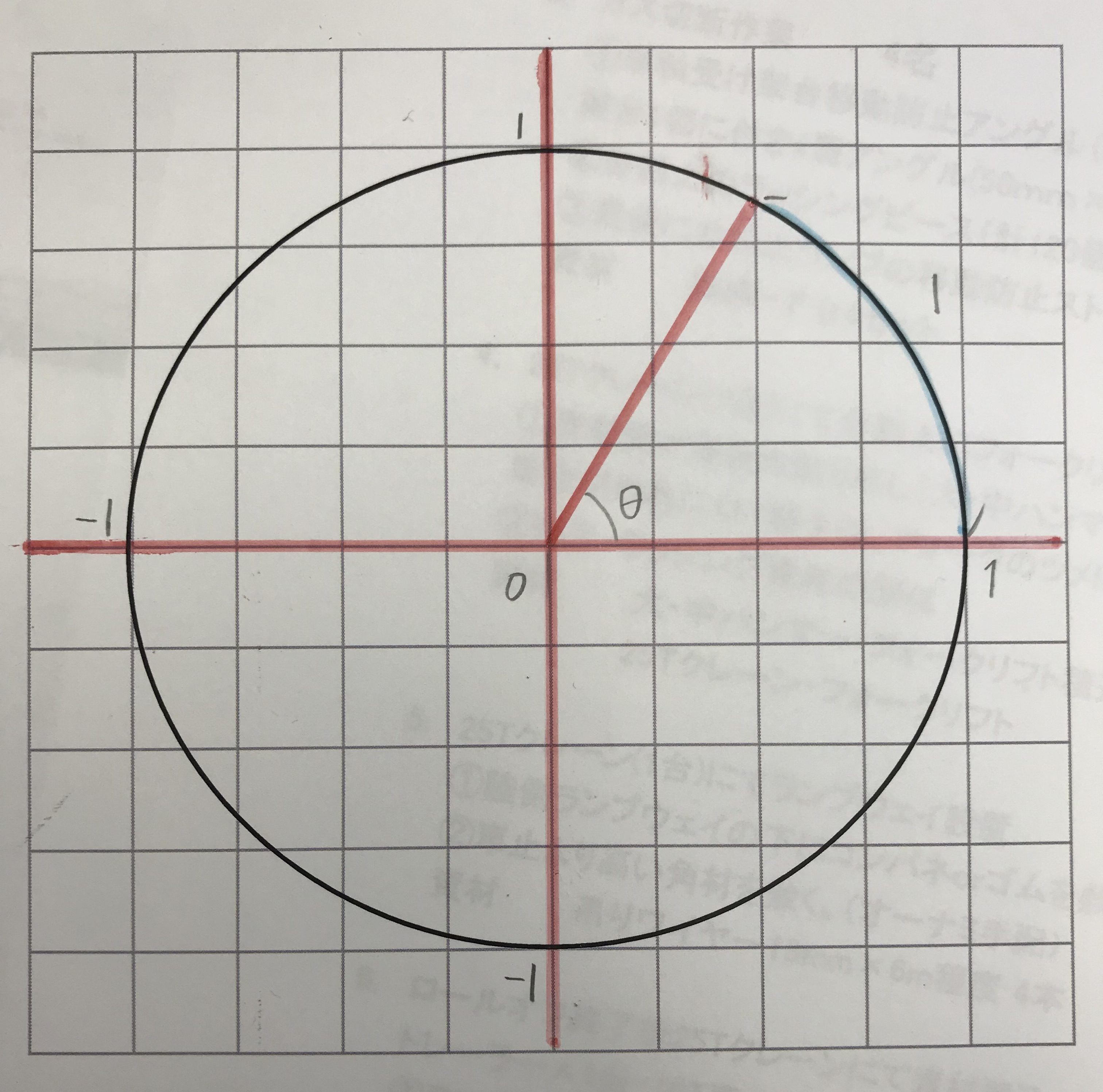
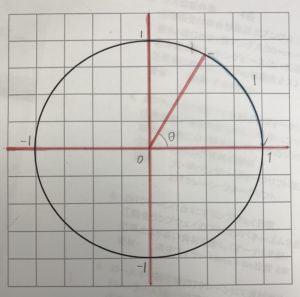
半径1の単位円で考えます。

※1radはおよそ57.3°です。